僕は趣味で競技プログラミング（競プロ）に取り組んでいます。
競技プログラミングをはじめたきっかけは、テレビで紹介されているのを見ておもしろそうだなと感じ、プログラミングのスキルアップに繋がりそうだと感じたためです。
すでに1年半ほど続けており、AtCoder（競技プログラミングコンテスト）でのレートは 1,800 ほどです。レートごとに色分けされていて、自分のレート帯は青コーダーと呼ばれており、結構強いです！
ちなみにどれくらいの強さかというと、週に1度開かれるコンテストで、約10,000人中 200位～800位の順位をとれる程度です。
こちらが私のAtCoderアカウントです。
https://atcoder.jp/users/yuuki_n
競技プログラミングでは、数列に対する操作について求められる問題が多く、それらの問題を解答する上で使える初歩的なテクニックとして「累積和」を紹介させていただきます。
より複雑なアルゴリズムがあり、それらの基礎となる考え方について学べますので、是非参考にしてください。皆さんがこの記事を読んで、競技プログラミングをはじめるきっかけになれば嬉しいです。
累積和でできること
長さnの配列aのある区間[l,r)※1の総和を求める処理を高速に行うことができます。元の配列のままで、ある区間の総和を求める場合、その区間の長さに比例する計算量が必要ですが、累積和を用いることで1回の計算で区間の総和を求めることができます。
※ただし、前計算として累積和を管理する配列を構築する必要があり、これは配列の長さに比例する回数の計算が必要です。
そのため、ある配列aに対して、区間の総和を求める処理を複数回行いたい場合に役に立ちます。
1.累積和の仕組み
累積和の仕組みは簡単です。累積和を管理する配列sumで以下のようにsum[i]が配列aの前からi個の総和を持つようにします。
sum[0] = 0
sum[1] = a[0]
sum[2] = a[0] + a[1]
…
sum[n] = a[0] + a[1] + … + a[n-1]
例 a = {3,1,4,1,5,9,2,6,5}の時
sum = {0,3,4,8,9,14,23,25,31,36}となります。
ここで、区間[1,6)の総和を求めてみましょう。
配列sumを観察すると
sum[1] = a[0]
sum[6] = a[0] + a[1] + a[2] + a[3] + a[4] +a[5]
となっており、この差はa[1] + a[2] + a[3] + a[4] +a[5]で区間[1,6)の総和となっています。
このことから、sum[6] – sum[1]の1回計算を行うことで区間[1,6)の総和を求めることができます。
一般に区間[l,r)の総和を求める場合、sum[r] – sum[l]で求めることができます。
元の配列のまま区間[1,6)の総和を普通に求めようとする場合
a[1] + a[2] + a[3] + a[4] +a[5]
= 1 + 4 + 1 + 5 + 9
= 20
と4回の足し算を行う必要があります。
2.実装
具体的な実装を紹介します。2.1 前計算
累積和を管理する配列を構築します。
これはsum[i+1]がsum[i]にa[i]を加えたものであることを使って前から順に埋めていくことができます。
実装はこのような感じです。
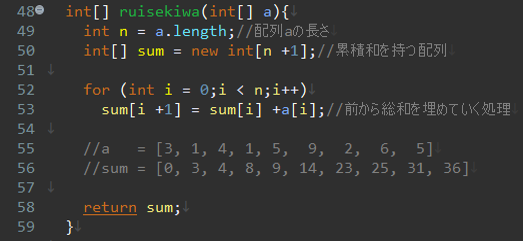2.2 区間の総和の取得
区間の総和を求める方法は先ほど紹介した通りに引き算をするだけです。
累積和を使った例題
以下のような問題を考えます。問題 1からNの番号がついたN個の重りがあり、番号iの重りの重さはW_iです。
ある整数
1≤T<Nに対してこれらの重りを番号が T 以下の重りと番号が T より大きい重りの2グループに分けることを考え、それぞれのグループの重さの和をS_1,S_2とします。
このような分け方全てを考えたとき、S_1とS_2の差の絶対値の最小値を求めてください。
制約 ・2≤N≤100
・1≤W_i≤100
・入力は全て整数である
https://atcoder.jp/contests/abc129/tasks/abc129_b
解法 Tとしてありうる番号をすべて試し、差の絶対値をシミュレーションで求めます。それらの最小値を答えます。
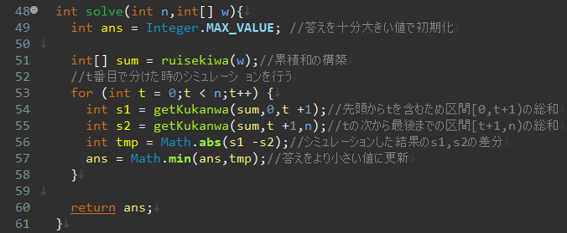※実は制約のNの値が小さいため、累積和を用いらずに毎回、愚直に足し算を使って、S_1,S_2を求めても間に合います。Nが10万程度であったり、前後2分割ではなく4分割くらいにして、それらの区間の総和の最大値-最小値の最小値を求める場合は、高速化が必要になってきます。
※1 区間は競技プログラミングではよく[l,r)のように半開区間で表します。これは数列のl番目からr-1番目までのことです。半開区間のため右側の添え字rの位置は含みません。
例 数列{3,1,4,1,5,9} の区間[1,4)は{1,4,1}となり、総和は6です。
以上になります。今回は初投稿なので、比較的簡単なアルゴリズムを紹介しました。
累積和では、配列に対して値の変更がある場合は対応できないのですが、値についてご紹介する機会があれば、変更にも対応できるデータ構造の紹介をしようと思っています。
おわりに
直接業務の役に立つ機会は少ないのですが、僕は競技プログラミングをはじめてから、要件や仕様を理解する時間が速くなったように思います。加えて、プログラムの実装をする際には、細かいミスも減ったなとも感じてます。また、SNSをはじめるきっかけにもなり、共通の趣味や興味のあることが似ている友人が増えたことも競技プログラミングをはじめて良かったことのひとつです。
最後までお読みいただきありがとうございました。
